2024-05-02
639次浏览 发布时间:2024-02-21 17:15:56 编辑: 闻讯百通
高斯(Carl Friedrich Gauss)是历史上最伟大的数学家之一,他创造了许多影响深远的数学成果。但是,高斯不仅仅是一位杰出的数学家,他还拥有着敬畏人物的奇妙人生。本文将介绍高斯的传奇人生及其标志性的数学成果。

高斯生于1777年的德国布伦瑞克,他的父母是德国普鲁士王国的下层贵族,而他的母亲则非常聪明,擅长于数学和哲学。成长于如此丰富的智力环境下,高斯从小就表现出超凡的数学才华,并在13岁时发明了一个方法来计算求和公式。该公式为:S = [n(a + l)] / 2,其中,S表示等差数列的总和,n表示等差数列中项的个数,a表示等差数列的第一项,l表示等差数列的最后一项。
这个公式可以极大地简化等差数列求和的计算,对于当时的数学界来说具有重要的意义。这也标志着高斯在数学领域的开端。
高斯成年后,在学院里学习了天文学和物理学。在学习期间,他发明了高斯消元法,这种方法被广泛应用于科学和工程领域中解决线性方程组的问题。高斯消元法的应用范围非常广泛,无论是计算机图形处理还是建筑设计,都需要用到这个方法。
高斯消元法:

高斯消元法是一种求解线性方程组的方法。该方法基于列主元原理,将系数矩阵化为行简化阶梯矩阵,从而可以用反向代换法求解方程组。
高斯的数学功绩不仅仅止于高斯消元法,同时还包括了微分几何、概率论以及数论等方面的重要研究成果。尤其是他的研究成果,为数论的发展做出了突出的贡献。他为代数数论开辟了道路,发现了素数分布的规律,提出了二次剩余的概念等。二次剩余是数论中的一个重要概念,它涉及到模运算和欧拉定理等数学知识。
在模数为素数 P 的情况下,如果存在整数 X 满足 ,则称
,则称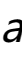 是模
是模 的二次剩余。当 X 的取值不同时,所有的二次剩余所构成的集合被称为关于模 P 的二次剩余系。二次剩余理论在数论、密码学和计算机科学等领域广泛应用。其中,RSA公钥加密算法就是基于大素数的二次剩余难题而设计的,而在密码学中常常使用离散对数问题来实现安全的加密算法,二次剩余理论则为解决离散对数问题提供了一些有效的途径。
的二次剩余。当 X 的取值不同时,所有的二次剩余所构成的集合被称为关于模 P 的二次剩余系。二次剩余理论在数论、密码学和计算机科学等领域广泛应用。其中,RSA公钥加密算法就是基于大素数的二次剩余难题而设计的,而在密码学中常常使用离散对数问题来实现安全的加密算法,二次剩余理论则为解决离散对数问题提供了一些有效的途径。

高斯对数学的热爱和追求使得他在数学领域中成为一位天才,他发掘出的数学规律和公式也成为当今数学领域的重要组成部分,其中四个高斯公式都是他的重要贡献,这些公式的发明使得高斯成为了当代数学领域最具标志性的人物之一。
高斯定理是高斯在物理学和电学领域的研究成果之一,是电场和电荷密度之间的一种关系,在静电学和电动力学中都有重要应用;高斯消元法则是现代科学和工程学科中不可或缺的一个元素,可以解决大量实际问题;高斯-马克思维尔定理是高斯对电磁学的贡献之一,揭示了磁场和电荷的关系,被广泛应用于天体物理学、核物理学和化学等领域;而高斯-斯托克斯定理则用于描述多种物理量之间的关系,在流体力学、电磁学等领域都有着重要的应用。
高斯-马克思维尔定理:

该公式描述了电场的散度性质,并且说明了电荷密度与电场之间的关系。这个定理对电学、磁学甚至是光学都有很大的应用价值,被视为电动力学的基础之一。
高斯-斯托克斯公式:
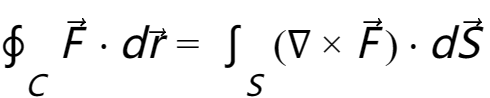
该公式指出,如果在三维空间中有一个向量场 ,则向量场通过某个封闭曲面
,则向量场通过某个封闭曲面  的积分等于该曲面所包围的体积内部上,向量场旋度的通量。这条定理不仅应用广泛,还是在数学和物理学中的基本公式之一。
的积分等于该曲面所包围的体积内部上,向量场旋度的通量。这条定理不仅应用广泛,还是在数学和物理学中的基本公式之一。
除了对数学的热爱以外,高斯还在地理学和统计学领域作出了杰出贡献。1786年时,高斯就开始计算地球的形状和大小,最终他发现地球是一个椭圆体,这项贡献为测量和导航提供了基础,受到了世界各国的认可。同时,高斯在统计学领域也有很深入的研究,他发明了高斯分布(正态分布),并通过率先使用误差范围概念,成为概率论早期研究成果之一,有着广泛的应用领域。
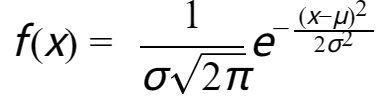
其中,e是自然对数的底数,π是一个圆的周长与直径的比值,σ是标准差,μ是均值,x是随机变量。

高斯分布在实际应用中非常广泛,例如在统计学、物理学、金融学和机器学习等领域。其重要性在于中心极限定理可以用来证明,许多随机变量的和在趋向于正无穷或负无穷时,其随机分布将趋近于高斯分布。同时,高斯分布的可靠性和精度也是其得到广泛应用的原因之一。
但是,高斯不仅仅是一位天才的数学家,同时也是一位热心肠的人道主义者。他对他人的错误持宽容态度,对自己也非常严苛。他在日记中写道:“我好像没有多大的天赋,只是一路勤奋而已。”在1835年去世之前,高斯一生中也曾经历过很多悲痛和困难,但是他依旧能够坚持自己执着的信念,并一直在为人类的进步做出贡献。
总之,高斯既是一位天才的数学家,同时也是一位热心肠的人道主义者。他的数学成就为当今的数学界做出了重大贡献,并且他的生平和思想更是蕴含着非常深刻的启示。人们有理由称他为“数学巨星”,以及享有永恒的传奇地位。